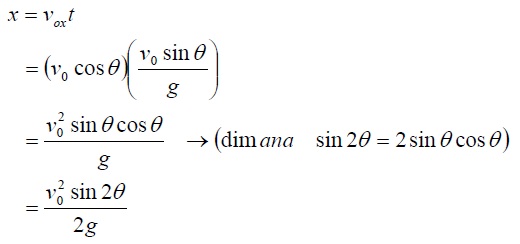Gerak peluru atau disebut juga sebagai gerak parabolik, merupakan gerak yang terdiri dari gabungan GLB pada arah sumbu horizontal dan GLBB pada arah sumbu vertikal. Jadi untuk setiap benda yang diberi kecepatan awal sehingga menempuh lintasan gerak yang arahnya dipengaruhi oleh gaya gravitasi yang bekerja terhadapnya dan juga dipengaruhi oleh gesekan udara, benda tersebut disebut mengalami gerak peluru. Misalnya saja seperti bom yang dijatuhkan dari pesawat terbang, bola yang dilontarkan atau dipukul, misil yang ditembakkan oleh meriam, dan roket yang sudah kehabisan bakarnya.


Proyeksi Gerak Peluru
Proyeksi Gerak Peluru
Gambar diatas menunjukkan proyeksi gerak peluru pada sumbu horizontal (sumbu x) dan sumbu vertikal (sumbu y), dengan titik pangkal koordinatnya ada pada titik dimana peluru tersebut mulai terbang bebas. Pada titik pangkal tersebut ditetapkan t = 0 dengan kecepatan awal yang digambarkan dengan vektor v0 yang membentuk sudut elevasi θ⁰ terhadap sumbu x.
Persamaan -Persamaan Gerak Peluru

Kecepatan awal diuraikan menjadi komponen horizontal v0x dan voy yang besarnya :

v0x = v0 cos θ , dan
v0y = v0 sin θ

Karena komponen kecepatan horizontal konstan, maka pada setiap saat t akan diperoleh :

vtx = v0x + at = v0x + (0)t = vox = v0 cos θ
dan
x = v0xt + ½at2 = voxt + ½(0)t2 = v0xt

Sementara itu, percepatan vertikal adalah –g sehingga komponen kecepatan vertikal pada saat t adalah :

vty = voy – gt = vo sin θ – gt
y = voyt – ½gt2
v2ty =v20y – 2gy

Persamaan diatas berlaku jika peluru ditembakkan tepat pada titik awal dari sistem koordinat xy sehingga x0 = y0 = 0. Tetapi jika peluru tidak ditembakkan tepat pada titik awal koordinat (x0 ≠ 0 dan y0 ≠ 0), maka kedua persamaan tersebut menjadi :
x = x0 +v0xt = x0 + (v0 cos θ)t
y = y0 +voyt – ½gt2
Pada titik tertinggi artinya pada posisi y maksimum, maka kecepatannya adalah horizontal sehingga vty = 0. Sehingga persamaan diatas menjadi
vty = voy -gt
0 = voy – gt
t = \frac{v_{oy}}{g}
t = \frac{v_{o}sin\theta}{g}
Persamaan diatas menunjukkan waktu yang dibutuhkan untuk mencapai ketinggian maksimum. Kemudian subtitusikan ke persamaan (y) sehingga diperoleh persamaan ketinggian maksimum sebagai berikut :


Subtitusi persamaan (t) ke persamaan (x) akan menghasilkan posisi x pada saat y maksimum, yaitu :

Sedangkan pada titik terjauh dari titik awal artinya posisi x maksimum, maka waktu yang dibutuhkan untuk mencapai x maksimum adalah :

t = \frac{2 v_{o}sin\theta}{g}

Dan posisi terjauh atau x maksimum adalah :

xm = \frac{2 v_{o}^{2} \text { sin }\theta}{2g}  =  \frac{v_{o}^{2} \text { sin }\theta}{g}

 sumber : http://fisikazone.com/gerak-peluru/persamaan-gerak-peluru/

Leave a Reply